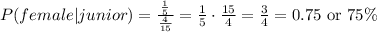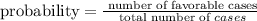
Total number of students = 4 + 6 + 2 + 2 + 3 + 4 + 6 + 3 = 30
The probability that a student is female given that it is a junior is computed as follows:
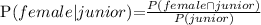
The probability that a student is female and junior is:
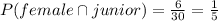
The probability that a student is a junior is:
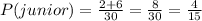
Finally, The probability that a student is female given that it is a junior is: