In part a we must find the inverse of:
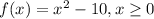
For this purpose we'll need to make the following replacements:

With these replacements we get:

So we need to solve this equation for f^(-1):

We add 10 at both sides of the equation:
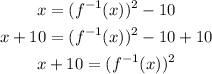
Now we apply the square root at both sides:
![\begin{gathered} x+10=(f^(-1)(x))^2 \\ √(x+10)=\sqrt{(f^(-1)(x))^2} \\ f^(-1)(x)=\sqrt[]{x+10} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/vzgd0u36vx4sbngfx505wux9eplxm9spuo.png)
So the answer to part a is:
![f^(-1)(x)=\sqrt[]{x+10}](https://img.qammunity.org/2023/formulas/mathematics/college/832kvczc7vf3z63auoal2vvbjmcphwa87n.png)
In part b we must find the domain and range of both f and f^(-1). The domain is composed of all the possible x values for which the function ha