Question

Solve by graphing. If the population of a town is growing at a rate of 2.5% each year and the current population is 50,000. After how many years will the population reach 100,000 people. Round to the NEAREST whole number. Be sure to label your answer.

Answer 1

The situation describes an exponential growth, which can be expressed using the general formula:

`y=a(1+r)^x`

Where

a is the initial value

r is the growth rate, expressed as a decimal value

x is the number of times intervals

y is the final value after x time intervals

For the studied population, the growth rate is 2.5%, to express this number as a decimal value you have to divide it by 100:

`\begin{gathered} r=(2.5)/(100) \\ r=0.025 \end{gathered}`

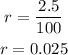
The initial value is the current population of the town: a=50000

You can express the equation of exponential growth for this population as follows:

`\begin{gathered} y=50000(1+0.025)^x \\ y=50000(1.025)^x \end{gathered}`

We know that after x years the population will be y=100000, to determine how many years it will take to reach this value you have to equal the equation to 100000 and solve for x:

`100000=50000(1.025)^x`

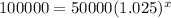
-Divide both sides of the expression by 50000

`\begin{gathered} (100000)/(50000)=(50000(1.025)^x)/(50000) \\ 2=(1.025)^x \end{gathered}`

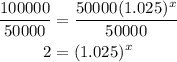
-Apply logarithm to both sides of the equal sign:

`\begin{gathered} \log (2)=\log (1.025^x) \\ \log (2)=x\cdot\log (1.025) \end{gathered}`

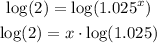
-Divide both sides by the logarithm of 1.025

`\begin{gathered} (\log(2))/(\log(1.025))=(x\cdot\log (1.025))/(\log (1.025)) \\ x\approx28.07\approx28 \end{gathered}`

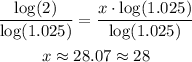
After approximately 28 years the population of the town will be 100,000.