Question

TRIGONOMETRY Find the magnitude of the resultant vector round to the nearest tenth

Answer 1

he formula to determine the magnitude of a vector (in two dimensional space) v = (x, y) is:

|v| =√(x2-x1)^2 + y2-y1)^2.

This formula is derived from the Pythagorean theorem.

`\begin{gathered} \bar{v}=(13.5,-21.07) \\ \bar{w}=(-0.9,-14.6) \end{gathered}`

`\begin{gathered} i=i_v-i_w \\ i=13.5--0.9 \\ i=14.4 \end{gathered}`
`\begin{gathered} j=j_v-j_w \\ j=-21.07--14.6 \\ j=-6.47 \end{gathered}`

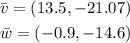
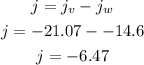
Therefore the magnitude of the resultant vector is

`\begin{gathered} |vw|=\sqrt[]{i^2+j^2} \\ |vw|=\sqrt[]{(14.4)^2+(-6.47)^2} \\ |vw|=15.787 \\ |vw|\cong15.79 \end{gathered}`

Therefore the magnitude of the resultant vector = 15.79 (nearest hundredth)