Recall the formula for continuously compounded interest:
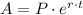
Where P is the principal (in our case $2711),
A is the accumulated total at the end of the investing period,
r is the annual interest rate (in our case 4.2% which in decimal form becomes: 0.042)
t is the time of the investment in years (in our case 11)
Then, we have:
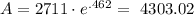
Then, the amount that is strictly the interest would be the difference:
4303.02 - 2711 = $1592.02