1 Answer

Ask a Question

Hashchen · Answer 1 · 2023-03-11T21:36:54+0000

Answer:

The standard deviation = 7.65

The variance = 58.55

Step-by-step explanation:

The given data are:

x = 19.9, 3.7, 24.6, 4.9, 13.5, 4.4, 19, 18.1

The mean is calculated as:

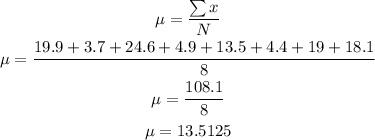
$\begin{gathered} \mu=(\sum x)/(N) \\ \mu=(19.9+3.7+24.6+4.9+13.5+4.4+19+18.1)/(8) \\ \mu=(108.1)/(8) \\ \mu=13.5125 \end{gathered}$

The standard deviation is given by the formula:

$\begin{gathered} SD=\sqrt{(\sum(x-\mu)^2)/(N)} \\ SD=\sqrt{((19.9-13.5125)^2+(3.7-13.5125)^2+(24.6-13.5125)^2+(4.9-13.5125)^2+(13.5-13.5125)^2+(4.4-13.5125)^2+(19-13.5125)^2+(18.1-13.5125)^2)/(8)} \\ SD=7.65 \end{gathered}$

The variance = SD²

The variance = 7.65²

The variance = 58.55

0 Comments

Please log in or register to add a comment.

Please log in or register to answer this question.

1 Answer

0 Comments

Please log in or register to add a comment.

Other Questions