Question

4) Shreya's school is selling tickets to a fall musical. On the first day of ticket sales the school sold

13 adult tickets and 9 student tickets for a total of $138. The school took in $163 on the second
day by selling 3 adult tickets and 14 student tickets. Find the price of an adult ticket and the
price of a student ticket. Find the price of and adult ticket and the price of a student ticket?

Answer 1

• adult: $3
• student: $11

Explanation:

Let x and y represent the prices of adult and student tickets, respectively. Then the revenue equations are ...

13x +9y = 138

3x +14y = 163

Solving this using a graphing calculator, we find (x, y) = (3, 11).

The price of an adult ticket is $3; the price of a student ticket is $11.

_____

Algebraic solution

When the numbers are "messy," as they are here, I like to use the "cross-multiplication method" for solution. I find it easier to use the order 1, x, y, rather than the order x, y, 1 as shown in the second attachment. That way, the coefficients are in their original order, with the first coefficient repeated. Note the right-side constant must be subtracted to get the form ax+by+c = 0.

`\begin{array}{cccc}13&9&-138&13\\3&14&-163&3\end{array}`

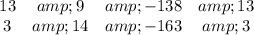
Then we have ...

1/(13·14 -3·9) = x/(9·(-163) -14·(-138)) = y/((-138)·3 -(-163)·13)

x = 465/155 = 3 . . . . price of an adult ticket

y = 1705/155 = 11 . . . price of a student ticket