Proportional relationships are relationships between two variables where their ratios are equivalent. Another way to think about them is that, in a proportional relationship, one variable is always a constant value times the other. That constant is know as the "constant of proportionality".
If the relationship between x and y is proportional, we can write a rule correlating them as
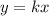
Where k is a constant.
From the table, we have the following values
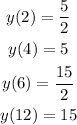
If we substitute the first expression on our form, we have the following constant of proportionality

If this is a proportional relationship, the constant of proportionality is 5/4. Let's check if this constant fits for the other values:
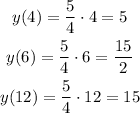
Since it fits, we have indeed a proportional relationship where 5/4 is the constant of proportionality.