In the given figure :
AB is height of the flagpole : AB = 25 feet
BC is the length of shadoe : BC = 42 foot
and angle FAE is the angle that the sun hits the flagpolem : FAE = θ
Since, line AE and line BC are the staright horizontal line, so they are parallel
and the line FC act as a transversal
So, Angle ACB = Angle FAE by corresponding angle properties
Now for angle ACB : line AB is opposite to the angle and the line BC is adjacent
Apply the trignometri ratio of Opposite side to adjacent side i.e. tangent of the angle

Substitute the value and simplify :
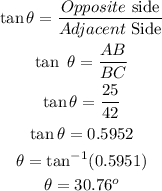
So, angle is 30. 76 degree
Angle FAE = θ = 30.76 degree
Angle FAE = 30.76 degree
The angle that the sun hits the flagpole is 30.76 degree
Answer : The angle that the sun hits the flagpole is 30.76 degree