Question

A Company manufactures and sells a specialty watch. The financial research department, using statistical methods, determined that a price of $88 each, the demand would be 2 thousand watches, and at $38 each, 12 thousand watches. Assuming a linear relationship in the form p(q) = mq + b. (a) What would be the price at a demand of 8 thousand watches? (b) 15 thousand watches?

Answer 1

Given:

a.) A price of $88 each, the demand would be 2 thousand watches.

b.) At $38 each, 12 thousand watches.

Since it was mentioned that the relationship is linear, we will be generating the equation in slope-intercept form (y = mx + b).

Let,

x = q = number of watches

y = p(q) = price of the watches

x1, y1 = 2,000, 88

x2, y2 = 12,000, 38

We get,

Step 1: The slope (m).

`\text{ m = }(y_2-y_1)/(x_2-x_1)\text{ = }\frac{\text{ 38 - 88}}{\text{ 12,000 - 2,000}}=\text{ }\frac{\text{ -50}}{\text{ 10000}}\text{ = -}\frac{\text{ 1}}{\text{ 200}}`

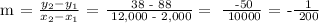
Step 2: Determine the y-intercept (b). Substitute x,y = 2,000, 88 and m = -1/200 in y = mx + b.

`\begin{gathered} \text{ y = mx + b} \\ \text{ 88 = (-}\frac{\text{ 1}}{\text{ 200}})(\text{2000) + b} \\ \text{ 88 = -}\frac{\text{ 2000}}{\text{ 200}}\text{ + b} \\ \text{ 88 = -10 + b} \\ \text{ b = 88 + 10} \\ \text{ b = 98} \end{gathered}`

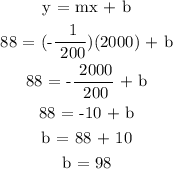
Step 3: Complete the equation. Substitute m = -1/200 and b = 78 in y = mx + b.

`\begin{gathered} \text{ y = mx + b} \\ \text{ y = (-}\frac{\text{ 1}}{\text{ 200}})\text{x + (98)} \\ \text{ y = -}\frac{\text{ 1}}{\text{ 200}}\text{x + 98} \\ \text{ p(q) = -}\frac{\text{ 1}}{\text{ 200}}\text{q + 98} \end{gathered}`

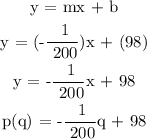
Question a: What would be the price at the demand of 8 thousand watches?

`\begin{gathered} \\ \text{p(q) = -}\frac{\text{ 1}}{\text{ 200}}\text{q + 98} \end{gathered}`
`\text{ p(8000) = -}\frac{\text{ 1}}{\text{ 200}}(8,000)\text{ + 98}`
`=\text{ - }\frac{\text{ 8,000}}{\text{ 200}}\text{ + 98}`
`=\text{ -40 + 98}`
`\text{ p(8,000) = 58 = \$58}`

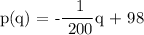
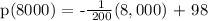
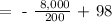
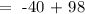
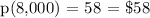
Therefore, at the demand of 8 thousand watches, the price will be $58.

Question b:

`\text{p(q) = -}\frac{\text{ 1}}{\text{ 200}}\text{q + 98}`
`\text{ p(15000) = -}\frac{\text{ 1}}{\text{ 200}}(15,000)\text{ + 98}`
`\text{ = -}\frac{15,000}{\text{ 200}}\text{ + 98}`
`=\text{ }-75\text{ + 98}`
`\text{ p(15,000) = }23\text{ = \$23}`

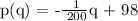
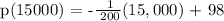
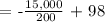
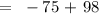
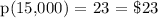
Therefore, at the demand of 15 thousand watches, the price will be $23.