Solution
The formula to find the equation of a straight line is
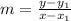
Given that the line passes through the point (-5,1) which is parallel to the given line
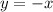
Since the lines are perpendicular, then to find the slope of the other line, the formula is
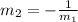
Let m₁ be the slope of the given line and m₂ be the slope of the line perpendicular to the given line
The general form of an equation of a straight line is
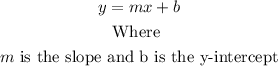
The slope, m₁, of the given line is -1, i.e m₁ = -1
The slope, m₂, of the line perpedicular to the given line will be
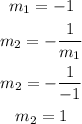
The slope, m₂, of the line passing through the points (-5, 1), m₂ = 1
Where
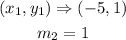
Substitute the variables into the formula to find the equation of a straight line
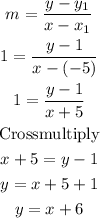
Hence, the equation of the line in slope-intercept form is
