The probability without replacement means that the total number of outcomes decreases by 1 after each selection. Also, we have to multiply the probability of each attempt.
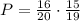
Observe, that the first attempt includes 16 possible events because there are 16 cards without 3, then, the second attempt includes 15 possibles and 19 total outcomes, that's because the card we selected first is not present in the deck.
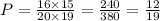
Hence, the probability of not getting a 3, without replacement is 12/19.
On the other hand, the probability with replacement is
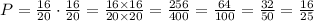
Hence, the probability of not getting a 3, with replacement, is 16/25.