We will determine it as follows:
*We can see that the triangle has the following vertex:
A(1, 3)
B(3, 7)
C(5, 3)
Now, we determine the directional segments:
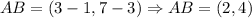
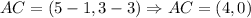
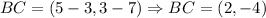
Now, we determine the distance of each segment:
![d_(AB)=\sqrt[]{2^2+4^2}\Rightarrow d_(AB)=2\sqrt[]{5}](https://img.qammunity.org/2023/formulas/mathematics/college/yapx6rbzde6zuzs1zv9131tr249wj0azoi.png)
![d_(AC)=\sqrt[]{4^2+0^2}\Rightarrow d_(AC)=4](https://img.qammunity.org/2023/formulas/mathematics/college/dify0ge5oledqk8xvk0y6a03b83zee1x4r.png)
![d_(BC)=\sqrt[]{2^2+(-4)^2}\Rightarrow d_(BC)=2\sqrt[]{5}](https://img.qammunity.org/2023/formulas/mathematics/college/vga1zs5m3dtg5n6t77phpj6abprqpsk869.png)
From this, we have that the triangle is isosceles.