To identify the inequality graphed you need to identify the equation of the line that limits the inequality:
To identify the equiation of the line you need to dinf the slope:
Use two points on the line: (0 , - 4) and (3,0)
Formula to find the slope:

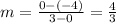
The y - intercept (b) is the value of y when x=0 in this case the b is -4
You have the equation in slope-interpcept form:
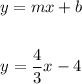
Substract -4/3 x in btoh sides of the equation:

Multiply both sides of the equation by 3:
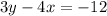
Multiply for -1 both sides of the equation:
Equation of the line:
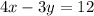
As the shadow area is under the line the inequality is:
