Let there are x moldavites, y amber, and z amethysts gemstones in the box. So equation for the total gemstones is,
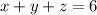
Equation from the weigh of the gemstones is,
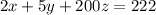
The equation for the cost of gemstones is,
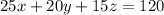
Simplify the equation x + y + z = 6 to obtain the value of y.
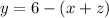
Substitute the value of y in the equation to obtain equation in x and z.
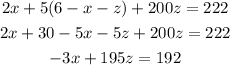
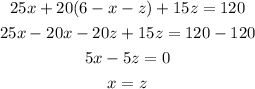
Substitute z for x in equation -3x + 195z = 192 to obtain the value of z.
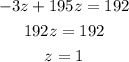
As, x is equal to z. So value of x is 1.
Substitute 1 for x and 1 or z in equation y = 6 - (x + y) to obtain the value of y.
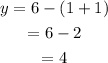
So there are 1 moldavites, 4 amber, and 1 amethysts gemsones in the box.