Problem 1
Answer: Choice A) The domain in interval notation is [2, 6]
Step-by-step explanation:
The domain is the set of allowed x inputs. For graphs, we look at the left-most point and right-most point. This tells us the boundaries of the domain. We go from x = 2 to x = 6, including both endpoints.
We can write the domain as this inequality
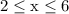 which condenses to the interval notation [2, 6]
which condenses to the interval notation [2, 6]
Make sure to use square brackets to include each endpoint.
Choice B is a trick answer since we won't be using roster notation. Roster notation is only useful for discrete domains, but this relation has a continuous domain.
==============================================
Problem 2
Answer: Choice B) The range in interval notation is [-4, 0]
Step-by-step explanation:
The range is the set of y values in a relation. Look at the lowest and highest points to determine the boundaries.
The lowest point occurs when y = -4, and the highest is when y = 0. The range is anything between these endpoints, including the endpoints themselves.
Therefore we get
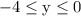 which condenses to [-4, 0]
which condenses to [-4, 0]
This time choice A is a trick answer because the range is continuous rather than discrete.