Question

A metal alloy is made by mixing Metal A and Metal B. If 100kg of the mixture contains 60% by mass of metal A and 40% by Mass of metal & Calculate the density of the metal alloy Give density of Metal A as 9000 kgm 3 and density of Metal B as 6000 kgm 3)

Answer 1

The density of the metal alloy is 7,496.25 kg/m^3 (rounded to 7,496 kg/m^3).

Step-by-step explanation:

The given information from the exercise is:

- Metal alloy mass (m): 100kg

- Mass of metal A (mA): 60kg

- Mass of metal B (mB): 40kg

- Density of metal A (dA): 9,000 kg/m^3

- Density of metal B (dB): 6,000 Kg/m^3

1st) With the values of mass and density of each metal, we have to calculate the volume of each metal:

• Volume metal A:

`\begin{gathered} V_A=(m_A)/(d_A) \\ V_A=(60kg)/(9,000(kg)/(m^3)) \\ V_A=6.67*10^(-3)m^3 \end{gathered}`

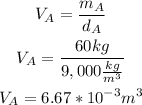
• Volume metal B:

`\begin{gathered} V_B=(m_B)/(d_B) \\ V_B=(40kg)/(6,000(kg)/(m^3)) \\ V_B=6.67*10^(-3)m^3 \end{gathered}`

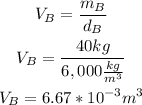
The volume of metal A and metal B is 6.67x10^-3 m^3. So, we have to add them to obtain the total volume of the metal alloy:

`\begin{gathered} V=V_A+V_B \\ V=0.00667m^3+0.00667m^3 \\ V=0.01334m^3 \end{gathered}`

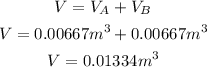
2nd) Now we can calculate the metal alloy density, replacing the values of Volume (V) and the metal alloy mass (100kg) in the density formula:

`\begin{gathered} d=(m)/(V) \\ d=(100kg)/(0.01334m^3) \\ d=7.496.25(kg)/(m^3) \end{gathered}`

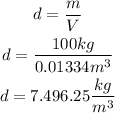
So, the density of the metal alloy is 7,496.25 kg/m^3 (rounded to 7,496 kg/m^3).