Hello there. To solve this question, we have to remember some properties about arithmetic sequences.
Given the first term of an arithmetic sequence and its common difference, we can determine the n-th term of the sequence using the following formula:

We know that a1 = 3 and d = 4, hence
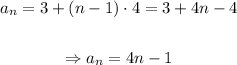
Is the general formula for the n-th term of the sequence.
Plugging n = 22, we find
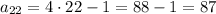
This is the 22nd term of this sequence.