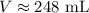Question

A small plastic vessel has the shape of a truncated cone as shown. Find the volume of the cup in millimeters

Answer 1

In this problem, we want to find the volume of a truncated cone, also knows as a frustum.

There are a couple of different methods we can use for this, including a general formula that can be applied.

We are given the following information:

- the diameter of the large base

- the diameter of the small base

- the height of the frustum

Since we don't know what the original height of the cone was before the frustum was created, we won't be able to use the method of subtraction (total volume minus volume of the removed smaller cone).

However, there is a useful formula we can use:

`V_{\text{ frustum}}=(\pi)/(3)\cdot h\cdot(R^2+r^2+Rr)`

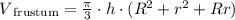
Where R represents the large radius, r represents the small radius, h represents the height.

Since we are given the diameter, we know the two radii will be half those values.

The large radius (marked in red) is

`(6.4)/(2)=3.2\text{ cm}`

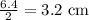
The small radius (marked in blue) is

`(4.8)/(2)=2.4\text{ cm}`

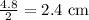
Finally, the height is 10 cm.

Caution! We are told to give our answer in milliliters! Make sure you write your final units that way.

`V=(\pi)/(3)(10)(3.2^2+2.4^2+3.2*2.4)`

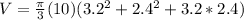
Using our calculator, we get the following approximation:

`V\approx248\text{ mL}`