Question

A rope pulls a 72.5 kg skier up a 21.7° slope with μk = 0.120. The rope is parallel to the slope, and exerts a force of 383 N. What is the acceleration of the skier?(Unit = m/s2)

Answer 1

`\begin{equation*} 0.567m\/s^2 \end{equation*}`

Step-by-step explanation

Parameters given:

Mass of skier, m = 72.5 kg

The angle of the slope, θ = 21.7°

Coefficient of kinetic friction, μk = 0.120

Force exerted, F = 383 N

Let us first make a sketch of the problem:

The net force acting on the skier is equal to the difference in the force exerted on the skier by the rope, the component of the weight parallel to the slope, and the force of friction:

`F_(net)=F-F_f-W\sin\theta`

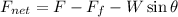
That is:

`F_(net)=383-\mu_kN-W\sin\theta`

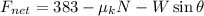
The free-body diagram is given below:

The normal force to the surface is given by:

`N=W\cos\theta`

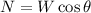
Therefore, the net force is:

`\begin{gathered} F_(net)=383-(0.120*72.5*9.8*\cos21.7)-(72.5*9.8*\sin21.7) \\ F_(net)=383-79.2178-262.7051 \\ F_(net)=41.0771N \end{gathered}`

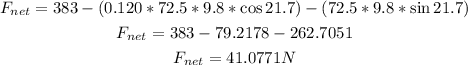
The net force is equal to the product of the mass of the skier and the acceleration of the skier. This implies that:

`F_(net)=m*a`

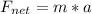
Solving for a:

`\begin{gathered} a=(F_(net))/(m) \\ a=(41.0771)/(72.5) \\ a=0.567m\/s^2 \end{gathered}`

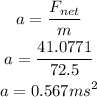
That is the acceleration of the skier.