Considering the random sample selected from a normal distribution:
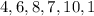
You have to construct a 99% confidence interval for the population mean μ
To construct the interval, considering that the same size is small (n = 6) and the population has a normal distribution, you have to use the student's t, which has the following formula:
![t=\frac{\bar{X}-\mu}{\frac{S}{\sqrt[]{n}}}\approx t_(n-1)](https://img.qammunity.org/2023/formulas/mathematics/college/njiy7qi5k033oassdma57zif1tt0uyscv0.png)
The formula for the confidence interval is:
![\lbrack\bar{X}\pm t_{n-1;1-(\alpha)/(2)}\cdot\frac{S}{\sqrt[]{n}}\rbrack](https://img.qammunity.org/2023/formulas/mathematics/college/79ao4s0rde1qi9j4rmbpbj59fef7ub06pt.png)
Where
X[bar] is the sample mean
S is the sample standard deviation
n is the sample size
t is the value of the statistic.
Before calculating the confidence interval, you have to calculate the sample mean and standard deviation:
Sample mean:
The formula for the sample mean is the following:
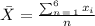
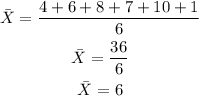
The sample mean is 6
Sample standard deviation:
The sample standard deviation is the square root of the sample variance. So you have to calculate the sample variance first and then the standard deviation:
Variance
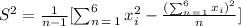
You have to make some auxiliary calculations:
Sum of squares of the observations:
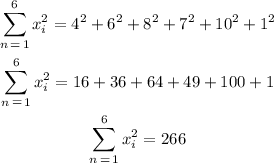
The sum of the observations was already obtained when we calculated the mean, it is:
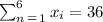
Replace the values on the formula of the variance:
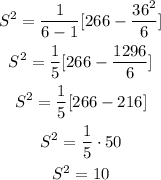
Apply the square root to obtain the sample standard deviation
![\begin{gathered} S=\sqrt[]{10} \\ S=3.16 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/brttdwhdp2stkxeikn016jx4dzikver6az.png)
Next, you have to determine the value of the statistic
The confidence level is 1-α=0.99
Calculate the value of α:
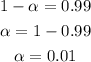
Divide it by 2
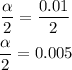
Subtract α/2 from 1 to determine the probability to use:

The value of the statistic is:
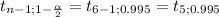
You have to use a value of the Student's t distribution with 5 degrees of freedom of 0.995 of probability.
The value is
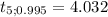
Next, calculate the confidence interval:
![\begin{gathered} \lbrack\bar{X}\pm t_{n-1;1-(\alpha)/(2)}\cdot\frac{S}{\sqrt[]{n}}\rbrack \\ \lbrack6\pm4.032\cdot\frac{3.16}{\sqrt[]{6}}\rbrack \\ \lbrack6\pm5.205\rbrack \\ \text{addition}\to11.205\approx11.20 \\ \text{subtraction}\to0.795\approx0.80 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/7fr58qa8sbqsszme617668bx6ew9j16eiz.png)
The confidence interval for the population mean is [0.80,11.20]
b.
For this part, you have to calculate a confidence interval using the same confidence level, the sample mean, and sample standard deviation but for a sample with a size of 25.
First, you have to determine the corresponding t-value for n=5 and 1-α=0.99

Sample mean X[bar]=6
Sample standard deviation S=3.16
n=25
![\begin{gathered} \lbrack X\pm t_{n-1;1-(\alpha)/(2)}\cdot\frac{S}{\sqrt[]{n}}\rbrack \\ \lbrack6\pm2.797\cdot\frac{3.16}{\sqrt[]{25}}\rbrack \\ \lbrack6\pm2.797\cdot(3.16)/(5)\rbrack \\ \text{addition}\to7.768\approx7.77 \\ \text{subtraction}\to4.231\approx4.23 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/bn3gcd8nofat472yn0n00le5r8oo08slk8.png)
The 99% confidence interval is [4.23,7.77]
The sample size and the width of the confidence interval have an indirect relationship, which means that when the sample size grows, the width shrinks. And when the sample size shrinks, the width grows.
The correct option is B. As the sample size increases, the width decreases.