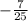We have that:
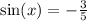
And with this information, we need to find the value of cos(2x).
To do this we use the following formula that relates sinx and cos(2x):
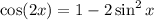
Substituting the value of sin(x):
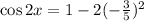
Now we need to solve the operations. We squared (-3/5) and we get (9/25):
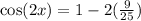
Next, we multiply 2 by (9/25) and get 18/25 instead:
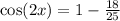
And finally, to make this substraction we consider 1=25/25
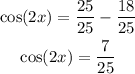
But, since we are considering that cos(x)<0 (is negative), then cos(2x) must also be negative, so the answer is: