Question

Use to reflect over the u-axis. Identify the transformed parallelogram.

Answer 1

So we have a matrix T that defines a transformation, more specifically a reflection over the y-axis:

`T=\begin{bmatrix}{-1} & 0 \\ 0 & 1\end{bmatrix}`

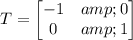
And we need to use to reflect:

`A=\begin{bmatrix}{3} & {4} \\ {-4} & {1}\end{bmatrix}`

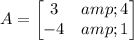
This basically means that we have to multiply both matrix. The result will be the matrix of the transformed parallelogram A':

`A^(\prime)=T\cdot A=\begin{bmatrix}{-1} & 0 \\ 0 & 1\end{bmatrix}\cdot\begin{bmatrix}{3} & {4} \\ {-4} & {1}\end{bmatrix}`

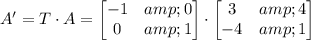
But first let's recal a property of the matrix product. Let's assume we have to multiply to nxn matrix B and C and the result of this multiplication is matrix D. The element in row i and column j of D is given by the product of row i of matrix B and column j of matrix C:

`d_(ij)=\sum ^n_(k\mathop=1)b_(ik)c_(kj)`

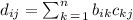
If we apply this to A' we have that the element on the first row and first column is given by multiplying the first row of T with the first column of A:

`A^(\prime)_(11)=(-1,0)\cdot(3,-4)=-1\cdot3-0\cdot4=-3`

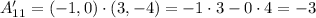
Then the element in the first row and second column is given by the product between the first row of T and the second column of A:

`A^(\prime)_(12)=(-1,0)\cdot(4,1)=-1\cdot4+0\cdot1=-4`

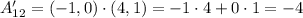
The element in the second row and first column is then:

`A^(\prime)_(21)=(0,1)\cdot(3,-4)=0\cdot3-1\cdot4=-4`

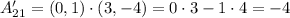
And finally the element in the second row and second column:

`A^(\prime)_(22)=(0,1)\cdot(4,1)=0\cdot4+1\cdot1=1`

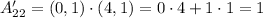
Then the matrix we are looking for is:

`\begin{bmatrix}{-3} & {-4} \\ {-4} & {1}\end{bmatrix}`

Then the answer is option C.