Question

Suppose a bowling ball is launched upwards from the top of a 270-foot building with an initial velocityof 80 ft/sec. The height in feet of the object t seconds later is given by thefunction h(t)= -16t² + 80t + 270.Find the x-intercepts of this function describe their meaning in the context of the problem, if any.Write your answer as a decimal rounded to 2 decimal places.Edit View Insert Format Tools Table12pt Paragraph v BIUA✓ ✓ T²vای

Answer 1

GIVEN:

A bowling ball is launched upwards from the top of a 270-foot building with an initial velocity of 80 ft/sec. The height in feet of the object t seconds later is given by the

function;

`h(t)=-16t^2+80t+270`

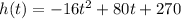
Required;

To find the x-intercepts of this function.

Step-by-step solution;

We are given the function that models the rise and then fall of a bowling ball launched from the top of a building. This means we have an upside down parabola. In other words, an upside down or downward opening parabola.

The x-intercepts of the equation of the parabola represents the points at which the curve crosses the x-axis.

Note the illustration of the "x-intercepts" as shown above.

To determine the x-intercepts, we note that these occur when the graph touches the y-axis at point zero. That means, when y = 0, the corresponding value is/are the x-intercept(s).

We will now re-write the function in the form of an equation as follows;

`y=-16t^2+80t+270`

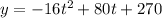
We now write the equation equal to zero;

`-16t^2+80t+270=0`

Now we solve for t;

`\begin{gathered} -16t^2+80t+270=0 \\ \\ Use\text{ the quadratic equation formula;} \\ \\ t=(-b\pm√(b^2-4ac))/(2a) \\ \\ Where;\text{ }a=-16,b=80,c=270 \\ \\ t=(-80\pm√(80^2-4(-16)(270)))/(2(-16)) \\ \\ t=(-80\pm√(6400+17280))/(-32) \\ \\ t=(-80\pm√(23680))/(-32) \\ \\ t=(-80\pm153.883072493)/(-32) \\ \\ t_1=(-80-153.883072493)/(-32),t_2=(153.883072493-80)/(-32) \\ \\ t_1=(-233.883072493)/(-32),t_2=(73.883072493)/(-32) \\ \\ t_1=7.30884601541,t_2=-2.30884601541 \end{gathered}`

Rounded to 2 decimal places, we now have the x-intercepts as follows;

ANSWER:

`x=-2.31,x=7.31`

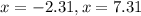
Further Explanation:

The x-intecepts in this context mean the points where the ball is at its minimum, or the point where the ball is at "ground level." Note that at the point where the ball is being thrown, its at ground zero. Then it takes off and, after a while it begins to fall and soon it falls to the point just parallel to the initial point of take off. These two points are the "x-intercepts" of the equation that models the bowling ball.