Question

Two buildings are 40 m apart, as shown below. From a point at the top of the shorter building, the angle of elevation to the top of the taller building is 37°. From the same point, the angle of depression to the foot of the taller building is 26°. Determine the height of the taller building, y. Round your answer to the nearest tenth. Do not use any symbols, letters or other notations in your answer other than an decimal point.

Answer 1

From the given figure, we can separate the diagram into two right-angled triagle as shown below

The figure is divided into right-angle trainle DAEand BAD. Please note that

`\begin{gathered} CD=x(\text{given)} \\ BE=y(given) \\ BC=40m(\text{given)} \\ CD=AB=x(opposite\text{ sides of a rectangle are equal)} \\ BC=AD=40m(\text{opposite sides of a rectangle are equal)} \\ AE=BE-AB=y-x \end{gathered}`

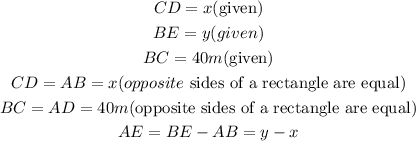
From triangle BAD, using trigonometry, we can solve for x

`\begin{gathered} \tan 26^0=(AB)/(AD) \\ \tan 26^0=(x)/(40) \\ x=40*\tan 26^0 \\ x=40*0.4877 \\ x=19.5093m \end{gathered}`

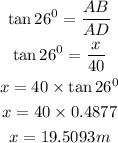
From triangle DAE, using trigonometry, we can solve for y

`\begin{gathered} \tan 37^0=(AE)/(AD) \\ \tan 37^0=(y-x)/(40) \\ y-x=40*\tan 37^0 \\ y-x=40*0.7536 \\ y-x=30.1422 \\ y=30.1422+x \end{gathered}`
`\begin{gathered} x=19.5093 \\ y=30.1422+19.5093 \\ y=49.6514m \\ y=49.7m(\text{nearest tenth)} \end{gathered}`

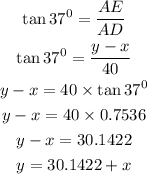
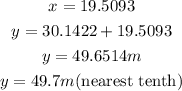
Hence, the height of the taller building is 49.7m