Question

Customers of a phone company can choose between two service plans for distance calls. The first plan has no monthly fee but charges 0.19 for each minute of callsThe second plan a $28 monthly fee and charges an additional $0.15 for each minute of callsFor how many minutes of will the costs of the two plans be equal?

Answer 1

Given:

Plan 1:

Charge for each minute = $0.19

Plan 2:

Monthly fee = $28

Charge each minute = $0.15

Let's determine when the costs of the two plans will be equal.

We have the following:

Equation for plan 1:

y = 0.19x

Equation for plan 2:

y = 0.15x + 28

Where x represents the number of minutes.

Now, to find when they will be equal, eliminate the equivalent sides y, then equate both expressions.

`0.19x=0.15x+28`

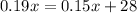
Let's solve for x.

Subtract 0.15x from both sides:

`\begin{gathered} 0.19x-0.15x=0.15x-0.15x+28 \\ \\ 0.04x=28 \end{gathered}`

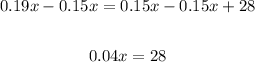
Divide both sides by 0.04:

`\begin{gathered} (0.04x)/(0.04)=(28)/(0.04) \\ \\ x=700 \end{gathered}`

Therefore, the two costs will be equal at 700 minutes.

ANSWER:

700 minutes