Question

A wheelchair ramp must form an angle no greater than 4.8 degrees with the ground. If a 1.8 foot high ramp is needed what is the minimum horizontal length for the ramp so it satisfies the angle requirement? Include a sketch of the ramp

Answer 1

21.44 feet

Explanations:

According to the question, we have the following information

Angle of elevation = 4.8degrees

Height off the ramp = 1.8 foot

Required

The minimum horizontal length for the ramp

The required sketch of the ramp is shown below:

From the diagram above, we can use the SOH CAH TOA identity to determine the value of horizontal length "x"

`\tan \theta=\frac{\text{opposite}}{\text{adjacent}}=(1.8)/(x)`

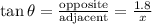
Substitute the given parameters

`\begin{gathered} \tan 4.8^0=(1.8)/(x) \\ x=(1.8)/(\tan 4.8^0) \\ x=(1.8)/(0.08397) \\ x\approx21.44\text{fet} \end{gathered}`

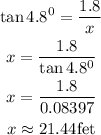
Therefore the minimum horizontal length for the ramp so it satisfies the angle requirement is approximately 21.44 feet