Question

I need help with this pls I need explanations as well.

Answer 1

Given:

`P(x)=x^9+2x^5-7x^3-x+2`

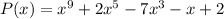
a) The degree of a polynomial is the highest of the degrees of the polynomial's monomials (individual terms) with non-zero coefficients.

The degree of P(x) is 9.

b) The polynomial P(x) will have 9 linear factors. It has degree 9, hence will have 9 roots or solutions. Each root can be made as a linear factor.

Therefore, the function P(x) will have 9 linear factors.

c) P(x) has 3 real solutions.

d) P(x) has 6 complex solutions.

e) Descartes rule of signs

Descartes's rule of signs is a rule for determining the maximum number of positive real number solutions (roots) of a polynomial equation in one variable based on the number of times that the signs of its real number coefficients change when the terms are arranged in the canonical order.

f) x = 2 is not a solution to P(x)

Applying the factor theorem,

`\begin{gathered} \text{If a is a root to a polynomial,} \\ \text{then, f(a)=0} \end{gathered}`

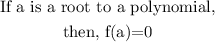
Thus,

`\begin{gathered} P(x)=x^9+2x^5-7x^3-x+2 \\ P(2)=2^9+2(2^5)-7(2^3)-2+2 \\ P(2)=512+2(32)-7(8)-2+2 \\ P(2)=512+64-56-2+2 \\ P(2)=520 \\ \\ S\text{ ince P(2)}\\e0,\text{ then x = 2 is not a solution.} \end{gathered}`

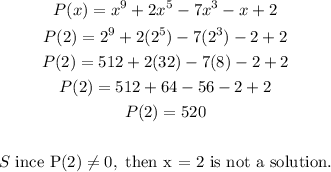
Therefore, x = 2 is not a solution to P(x)