Question

Find the half-life of a radioactive element, which decays according to the function A(t) = Ao exp( -0.0294t), where t is the timein years.

Answer 1

23.58 years.

Explanation:

The decay equation for the radioactive element is:

`A(t)=A_oe^(-0.0294t)\text{ where }\begin{cases}A(t)=\text{Amount at time t} \\ A_o=\text{Initial Amount}\end{cases}`

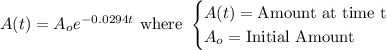
We want to find the half-life of the element.

The half-life of the radioactive substance is the time it will take for half of the initial amount of substance to decay. That is when:

`\begin{gathered} \text{Present Amount=}(1)/(2)\text{ of Initial Amount} \\ \implies A(t)=(1)/(2)A_o \end{gathered}`

Substitute A(t) into the formula.

`0.5A_o=A_oe^(-0.0294t)`

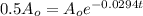
We then solve for t.

`\begin{gathered} \text{Divide both sides by 0.5} \\ (0.5A_o)/(A_o)=(A_oe^(-0.0294t))/(A_o) \\ e^(-0.0294t)=0.5 \\ \text{Take the natural logarithm of both sides} \\ \ln (e^(-0.0294t))=\ln (0.5) \\ -0.0294t=\ln (0.5) \\ \text{Divide both sides by }-0.0294 \\ (-0.0294t)/(-0.0294)=(\ln(0.5))/(-0.0294) \\ t=23.58\text{ years} \end{gathered}`

The half-life of the radioactive element is 23.58 years (correct to the nearest hundredth).