Question

A stone of mass 100g is projected upwards with an initial velocity of u. The stone reaches a maximum height of s. What initial velocity would the stone have to be projected with to reach a maximum height of 2s.2uu square root 24u8u

Answer 1

Answer:

u√2

Step-by-step explanation:

The mass, m = 100 g

m = 100/1000 g

m = 0.1 kg

Using the equation of motion below for upward motion

`\begin{gathered} v_f^2=v_i^2-2gH \\ \\ where: \\ v_f=final\text{ velocity} \\ \\ v_i=initial\text{ velocity} \\ \\ H=height \end{gathered}`

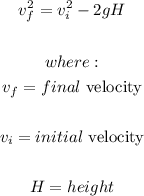
At maximum height, vf = 0 m/s

`\begin{gathered} 0=v_i^2-2gH \\ \\ v_i^2=2gH \\ \\ v_i=√(2gH) \end{gathered}`

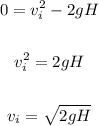
When maximum height, H = s, initial velocity = u

`v_i=√(2gs)\text{ = u}`

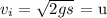
When maximum height, H = 2s

`\begin{gathered} v_i=√(2g(2s)) \\ \\ v_i=√(4gs) \\ \\ v_i=√(2)*√(2gs) \\ \\ v_i=√(2)u \\ \\ v_i=u√(2) \end{gathered}`

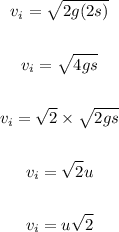
The initial velcoity that the stone has to be projected with to reach a maximum height of 2s = u√2