Question

An isosceles triangle has a base measuring 24 meters, and its two congruent sides each measure 15 meters. Find the area of thetriangle. (A=1/2 bh).

Answer 1

Let's start by illustrating the problem given to us. We have

What we want to look at first is the height of the triangle since it is the missing value to compute the area of the triangle. On the given illustration, we can divide the isosceles triangle into two right triangles. If the hypotenuse of the right triangle is given and its one side is also given, the measurement of the other side of the right triangle can be computed using the Pythagorean theorem

`\begin{gathered} a^2=c^2-b^2 \\ a=\sqrt[]{c^2-b^2} \end{gathered}`

The value of c here is 15 m, which is the hypotenuse, while b is 12 m, which is one side of the right triangle. Computing for the side a, which is the height of the triangle, we have

`a=\sqrt[]{15^2-12^2}=9m`

We now have the value of a, which corresponds to the height of the triangle. All we now have to do is to use the formula for the area of the triangle to solve the problem. We have

`A=(1)/(2)(24m)(9m)=108m^2`

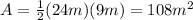
Therefore, the area of the isosceles triangle given is equal to 108 square meters.