Question

My app closed for no reason can you help me in this problem

Answer 1

a) We have the graph of f(x) and g(x).

The function g(x) seems to be the reflection of f(x) across the x-axis.

This can be represented mathematically as:

`\begin{gathered} g(x)=-1\cdot f(x) \\ g(x)=-f(x) \end{gathered}`

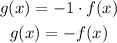
b) In this case, h(x) is f(x) rotated 180°.

The rule for this transformation is:

`(x,y)\longrightarrow(-x-y)`

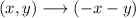
Both the value of the function h(x) as the argument, x, change signs, so we should get:

`h(x)=-f(-x)`

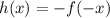
c) In this case, j(x) is the reflection of f(x) across the y-axis.

This can be represented as a change of sign in the argument x.

Then, we can write j(x) as:

`j(x)=f(-x)`

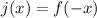
Answer:

a) g(x) = -f(x)

b) h(x) = -f(-x)

c) j(x) = f(-x)