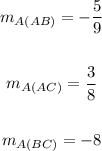An altitude in a triangle is a segment that goes from a vertex to the opposite side and it's perpendicular to it.
Knowing the vertices of the triangle ABC, you can draw the triangle on a Coordinate plane:
Now find the slope of each side using this formula:
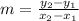
Then, you get:
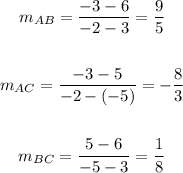
By definition, the slopes of perpendicular lines are opposite reciprocals. Knowing this, you can determine that the slopes of the altitudes on each side of triangle ABC are: