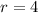Question

The equation of a circle is x^2+y^2-2x +6y-6=0. Find the center and radius of the circle by completing the square.you must include all steps. Your response must be at least 5-7 sentences at a minimum.

Answer 1

The center of the circle is at;

`(1,-3)`

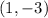
The radius of the circle is;

`r=4`

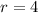
Step-by-step explanation:

Given the equation of circle;

`x^2+y^2-2x+6y-6=0`

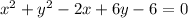
we want to re-write it in the form;

`(x-h)^2+(y-k)^2=r^2`

where;

`\begin{gathered} (h,k)\text{ is the center of the circle} \\ r\text{ is the radius} \end{gathered}`

Applying Completing the square method;

`\begin{gathered} x^2+y^2-2x+6y-6=0 \\ x^2-2x+1+y^2+6y+9=6+1+9 \\ (x-1)^2+(y+3)^2=16 \\ (x-1)^2+(y+3)^2=4^2 \end{gathered}`

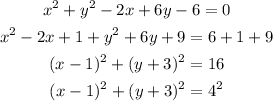
comparing the derived equation to the general form we have;

`\begin{gathered} h=1 \\ k=-3 \\ r=4 \end{gathered}`

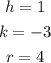
Therefore;

The center of the circle is at;

`(1,-3)`

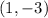
The radius of the circle is;

`r=4`