Question

TRIGONOMETRY Find the length of c round to the nearest tenth

Answer 1

Given:

A parallelogram ABCD.

To get the length of c, we have the sketch as shown below;

Using the side property of the parallelogram, opposite parallel sides are equal.

Hence,

`\begin{gathered} a=29^(\prime) \\ b=37^(\prime) \end{gathered}`

Also, using the angle property of a parallelogram, two adjacent angles are supplementary (add up to 180 degrees).

Hence,

`\begin{gathered} A+C=180^0 \\ 65+C=180 \\ C=180-65 \\ C=115^0 \end{gathered}`

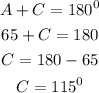
A triangle ABC can be brought out from the parallelogram,

To get the length of c, we use the cosine rule;

`\begin{gathered} c^2=a^2+b^2-2ab\cos C \\ \\ \text{where;} \\ a=29^(\prime) \\ b=37^(\prime) \\ C=115^0 \\ \\ \text{Hence,} \\ c^2=29^2+37^2-(2*29*37*\text{cos}115) \\ c^2=2210-(2146*\cos 115) \\ c^2=2210-(-906.9388) \\ c^2=2210+906.9388 \\ c^2=3116.9388 \\ c=\sqrt[]{3116.9388} \\ c=55.8296 \\ \\ To\text{ the nearest tenth,} \\ c=55.8^(\prime) \end{gathered}`

Therefore, the length of c to the nearest tenth is 55.8'