Let the rest mass of the baseball be m.
The Lorentz factor is given as,
![\gamma=\frac{1}{\sqrt[]{1-(v^2)/(c^2)}}\ldots(1)](https://img.qammunity.org/2023/formulas/physics/college/ydkev5lqrs7wefkdcb366zrnub1lmbgokf.png)
Here, v is the velocity of the object, and c is the speed of light.
The relative mass is given as,
![m_(rel)=\frac{m}{\sqrt[]{1-(v^2)/(c^2)}}](https://img.qammunity.org/2023/formulas/physics/college/rnwll1smsr2aq547r6zszjegik1w63fduo.png)
Using equation (1),
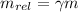
Substitute 2 for γ,
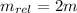
Therefore, the mass of the baseball relative to the ground is 2×m(baseball). Hence, option (A) is the correct choice.