The quadratic equation is:
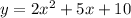
To find if the number of solutions, we use the discriminant of the equation. But first, we compare the given equation with the general quadratic equation:

By comparison, we find the values of a, b, and c:
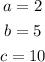
Now, as we said previously, we have to use the discriminant to find the number of solutions. The discriminant is defined as follows:
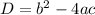
• If the value of D results to be equal to 0, there will be 1 real solution.
• If the value of D results to be greater than 0, there will be 2 real solutions.
• And if the value of D results to be less than 0, there will be no real solutions.
We substitute a, b and c into the discriminant formula:
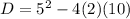
Solving the operations:
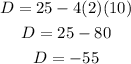
As we can see, the value of D is less than 0 (D<0) which indicates that there will be no real solutions for this quadratic equation.
Answer: No real solutions