Note that the work problem can be expressed in :
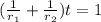
where r1 and r2 are the rates of work
and t is the time to complete 1 work.
From the problem, the rates are :
r1 = 8 hours
r2 = 6 hours
Using the formula above, we have :
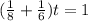
Solve for the value of t :
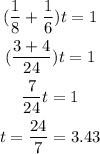
The answer is 24/7 or 3.43 hours.