Given:
The data is 45,69,72,76,78, 88,90, 96, 119, 145.
Step-by-step explanation:
Arrange the data in ascending order.
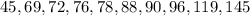
There are 10 term in the data. So median is average of (10/2)th term and (10/2 + 1)th term.
The (10/2)th term is 5the term which is 78 and (10/2+1)th term is 6th term which is 88. So median is,
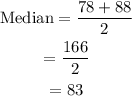
So median value is 83.
All values in data apperead only once. So there is no mode value for the given data.
The mean value is average value of the data, which is equal to sum of obsevation in data to the number of observation in the data. The mean value is,
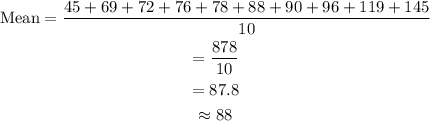
So mean value is 88.
The formula for the standard deviation is,
![SD=\sqrt[]{\frac{\sum ^(10)_(i\mathop=1)(\operatorname{mean}-x_i)^2}{N}}]()
Determine the standard deviation for the data.
![\begin{gathered} SD=\sqrt[]{((88-45)^2+(88-69)^2+(88-72)^2+(88-76)^2+(88-78)^2+(88-88)^2+(88-90)^2+(88-96)^2+(88-119)^2+(88-145)^2)/(10)} \\ =\sqrt[]{(1849+361+256+144+100+0+4+64+961+3249)/(10)} \\ =\sqrt[]{(6988)/(10)} \\ =\sqrt[]{698.8} \\ =26.4348 \end{gathered}]()
So standard deviation is 26.4348.
The range is difference of maximum and minimum value of data. SO range is,
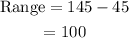
So range is 100.