We will first clear y from the second equation.
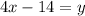
which is equivalent to

now, we change y by 4x-14 in the first equation and the solve for x.
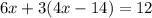

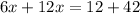
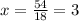
then x=3 and we replace it in the second equation to find the y value:
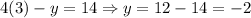
then the solution to this system of equations is the ordered pair (3,-2)