Proportional relationships are relationships between two variables where their ratios are equivalent. Another way to think about them is that, in a proportional relationship, one variable is always a constant value times the other.
Since the area of a circle is directly proportional to the square of the radius, their ratio should be maintained for different proportions, therefore, we have the following relation
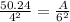
Where A represents the area of a circle with radius 6 ft. Solving for A, we have

The area is 113.04 ft².