Question

Graph the line with slope -3 through the point -3,3

Answer 1

Step-by-step explanation:

Here, we want to graph the line with the slope of -3 passing through the point (-3,3)

To graph the line, we need two points

We need the x-intercept (point on the x-axis where y = 0) and the y-intercept (point on the y-axis where x is 0)

The equation of a straight line can be represented as:

`y\text{ = mx + b}`

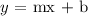
where m is the slope and b is the y-intercept

Using the equation above, we can write:

`y\text{ = -3x + b}`

We can get b by substituting the coordinates (-3,3: where -3 will be x and 3 will be y)

`\begin{gathered} 3\text{ = -3(-3) + b} \\ 3\text{ = 9 + b} \\ b\text{ = 3-9 = -6} \end{gathered}`

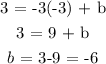
Now we have identified that the y-intercept is at he point (0,-6)

We have the full equation as:

`y\text{ = -3x-6}`

We need to get the x-intercept now.

We can get this by substituting the value 0 for y

Mathematically, we proceed as follows:

`\begin{gathered} 0\text{ = -3x - 6} \\ -3x\text{ = 6} \\ x\text{ = }(-6)/(3)\text{ = -2} \end{gathered}`

Thus, we have the x-intercept as (-2,0)

So to graph the line, we locate the points (0,-6) and (-2,0)

Then, we draw a line through these two points

This line will pass through the point (-3,3)