y - 4 = -1/2 (x +6) (option A)
Step-by-step explanation:
we apply the slope-form formula:

The points: (-6,4) and (2,0) = (x1, y1) and (x2, y2)
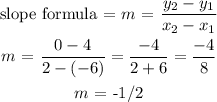
we pick any of the points and insert into the point-slope formula:
Using point (-6, 4)
y - 4 = -1/2 (x -(-6))
y - 4 = -1/2 (x +6)
Hence, the point-slope form of the equation below that represents the line that passes through the points (-6,4) and (2,0) is y - 4 = -1/2 (x +6) (option A)