The half-life of a radioactive element is given by
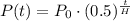
Where P(t) is the amount of element at time t, P₀ is the amount at time zero.
H is the half-life and t is the time in days.
For the given case,
t = 640 days
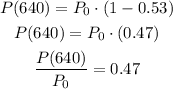
Now simply substitute this ratio into the above equation
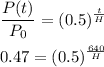
Take log on both sides
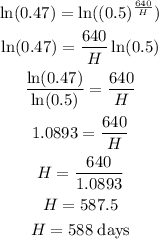
Therefore, the half-life of the element is 588 days
Part (b)
How long will it take for a sample of 100 mg to decay to 55 mg
So, we need to find time (t)
For the given case, we have
P(t) = 55
P₀ = 100
H = 588

Take log on both sides
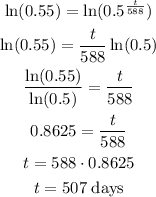
Therefore, it would take 507 days for a sample of 100 mg to decay to 55 mg.