Question

Winch2 inches12 inches

Answer 1

The figure appears to be a rectangular prism with the following dimensions:

Length = 12 inches

Width = 2 inches

Height = 3/4 inch

To be able to find the volume, we will be using the following formula:

`\text{ Volume = L x W x H}`

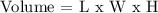
Where,

L = Length

W = Width

H = Height

We get,

`\text{ Volume = L x W x H}`
`\text{ = 12 x 2 x }(3)/(4)`
`\text{ = }\frac{\text{ 12 x 2 x 3}}{4}`
`\text{ = }(72)/(4)`
`\text{ Volume = 18 in}^3`

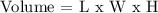
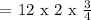
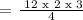
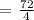
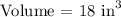
Therefore, the volume of the solid is 18 cubic inches.