You have to calculate the probability that the person after you orders a waffle cone sundae with vanilla ice cream and sprinkles.
Assuming that all choices are equally possible:
You have 3 cup choices: Cup(C), Sugar cone(S), or Waffle cone (W), the probability of choosing a waffle cone can be determined as follows:

There are two choices of ice cream: Vanilla (V), or Chocolate (C), the probability of choosing vanilla ice cream can be determined as follows:
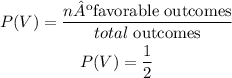
And there are three topping choices: Sprinkles (S), Hot Fudge (F), or Crushed cookies (C), the probability of choosing sprinkles can be determined as follows:

All options are independent, which means that the probability of choosing "waffle come and vanilla ice cream and sprinkles" is equal to the product of the individual probabilities of each choice:
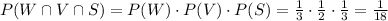
The probability is 1/18.