Question

The statement and the terminal point determined by is in quadrant 4

Answer 1

In this problem, we have an angle θ such that:

0. cot θ = 12/5,

,

1. sec θ = -13/5,

,

2. the terminal point determined by θ is in quadrant 4.

All the statements above cannot be true at the same time, and we must select the reason that explains this.

If we consider statement 3, the terminal point determined by θ is in quadrant 4, we must have an angle θ in the interval 270° < θ < 360°. If we compute the sec θ of the angles in this interval we see that we have:

`1<\sec \theta\text{ if }270^(\circ)<\theta<360^(\circ)\text{.}`

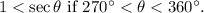
So we have sec θ greater than 1, and because of that, greater than zero too in quadrant 4. So it is impossible to have both statements 2 and 3 true at the same time.

Answer

B. cannot be true because sec θ is greater than zero in quadrant 4.