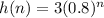Question

I don’t get the step by step please help me solve this

Answer 1

We know that each bounce reaches 80% of the height of the previous bounce.

So, when it has an initial height of 10 feet, the heights of the subsequent bounces are:

`\begin{gathered} n=1\colon10\cdot80\%=10\cdot0.8 \\ \\ n=2\colon(10\cdot0.8)\cdot80\%=10\cdot0.8\cdot0.8=10(0.8)^(2) \\ \\ n=3\colon(10\cdot0.8^2)\cdot80\%=10\cdot0.8\cdot0.8\cdot0.8=10(0.8)^(3) \end{gathered}`

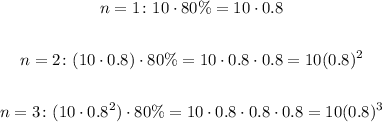
Thus, in the given function:

`h(n)=10(0.8)^n`

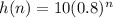
The number "10" stands for the initial height of the ball, in feet.

Therefore, if the ball is dropped from 3 feet, we need to replace 10 with 3. We obtain:

`h(n)=3(0.8)^n`