Question

A group of six sixth-graders measure and record their heights. The heights (in inches) are shown below.52, 62, 53, 61, 55, 53Find the mean and the median of the heights.The mean is ?The median is?

Answer 1

A group of six sixth-graders measure and record their heights.

The heights are 52, 62, 53, 61, 55, 53.

Mean : Mean is an average of the given numbers: a calculated central value of a set of numbers. It express as :

`\text{Mean =}\frac{Sum\text{ of all entries}}{Total\text{ number of entries}}`

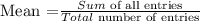
The given data has six sixth graders, So total number of entries = 6

Substitute the value :

`\begin{gathered} \text{Mean}=(52+62+53+61+55+53)/(6) \\ \text{Mean}=(336)/(6) \\ \text{Mean}=56 \end{gathered}`

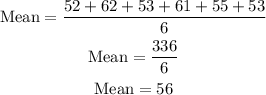
The mean of the recorded height is 56.

Median : It is the middle value of the given list of data, when arranged in an order.

The expression for the even number of observation is :

`\text{Meadian}=(((n)/(2))^(th)term+\mleft\lbrace(n)/(2)+1\mright\rbrace^(th)term)/(2)`

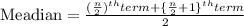
Arrange the given height in the ascending order.

52, 53, 53, 55, 61, 62

Since number of terms = 6

Substitute n = 6

`\begin{gathered} \text{Meadian}=(((6)/(2))^(th)term+\mleft\lbrace(6)/(2)+1\mright\rbrace^(th)term)/(2) \\ \text{Median}=(3^(th)term+4^(th)term)/(2) \\ \text{Median}=(53+55)/(2) \\ \text{Median}=54 \end{gathered}`

The median is 54

Answer :

Mean = 56

Median = 54