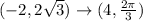Question

I need help with this practice problem solving Make sure to read the instructions as well

Answer 1

To transform rectangular coordinates to polar coordinates, we have the following relation between them

`\begin{gathered} \begin{cases}x={r\cos\theta} \\ y={r\sin\theta}\end{cases} \\ (x,y)\to(r,\theta) \end{gathered}`

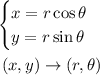
Then, we need to find the corresponding radius and the corresponding angle. First, to calculate the radius we can add the square of the rectangular coordinates. By the Pythagoras Theorem, the sum of the squares of the rectangular coordinates is equal to the square of the radius.

`x^2+y^2=r^2`

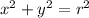
Using the given values, we have

`(-2)^2+(2√(3))^2=r^2`

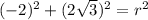
Solving for r

`\begin{gathered} (-2)^2+(2√(3))^2=r^2 \\ 4+4\cdot3=r^2 \\ 4+12=r^2 \\ 16=r^2 \\ r=√(16) \\ r=4 \end{gathered}`

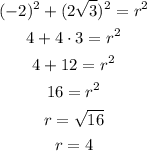
Then, we have our value for the radius. To calculate the angle, we can substitute the radius value on our expression to find the trigonometric relations of our angle.

`\begin{cases}-2={4\cos\theta} \\ 2√(3)={4\sin\theta}\end{cases}\implies\begin{cases}\cos\theta={-(1)/(2)} \\ \sin\theta=(√(3))/(2)\end{cases}`

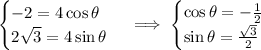
Since we have a negative cosine and a positive sine, our angle belongs to the second quadrant.

Applying the inverse function on one of those expressions, we get our angle.

`\begin{gathered} \arccos(\cos\theta)=\arccos(-(1)/(2)) \\ \theta=(2\pi)/(3) \end{gathered}`

Then, we have our polar coordinates.

`(-2,2√(3))\to(4,(2\pi)/(3))`